In applications where pseudo-random numbers are not appropriate,
one must resort to using a physical random number generator.
When using such a generator, it is essential to consider the
physical process used as the randomness source. This source
can be either based on a process described by classical physics
or by quantum physics. Classical physics is the set of theories
developed by physicists before the beginning of the XXth century
and which describes macroscopic systems like falling coins.
Quantum physics is a set of theories elaborated by physicists
during the first half of the XXth century and which describes
microscopic systems like atoms or elementary particles. Some
examples of generators based on each of these theories, along
with their advantages, are presented below, after a brief discussion
of biased random number sequences.
A problem encountered with physical random number generators
is their bias. A binary generator is said to be biased when
the probability of one outcome is not equal to the probability
of the other outcome. Bias arises because of the difficulty
to devise precisely balanced physical processes. It is however
less of a problem than one might expect at first sight. There
exists some post-processing algorithm that can be used to remove
bias from a sequence or random numbers.
The simplest of these unbiasing procedures was first proposed
by Von Neumann [1]. The random bits of a sequence are grouped
in subsequences of two bits. Whenever the two bits of a subsequence
are equal, it is discarded. When the two bits are different
and the subsequence starts with a 1, the subsequence is replaced
by a 1. When it starts with a 0, it is replaced by a 0. After
this procedure, the bias is removed from the sequence.
The cost of applying an unbiasing procedure to a sequence is
that it is shortened. In the case of the Von Neumann procedure,
the length of the unbiased sequence will be at most 25% of the
length of the raw sequence. It was mentioned above that randomness
tests basically all amount to verifying whether the sequence
can be compressed. An unbiasing procedure can be seen as a compression
procedure. After its application, the bias is removed and no
further compression is possible, guaranteeing that the sequence
will pass the tests. Other unbiasing procedures exist. The one
proposed by Peres [2] for example is significantly more efficient
than the Von Neumann procedure.
Macroscopic processes described by classical physics can be
used to generate random numbers. The most famous random number
generator – coin tossing – indeed belongs to this
class. However, it is very important to realize that classical
physics is fundamentally deterministic.
Processes described by quantum physics
randomness revealed by simplicity
Contrary to classical physics, quantum physics is fundamentally
random. It is the only theory within the fabric of modern physics
that integrates randomness. This fact was very disturbing to
physicists like Einstein who invented quantum physics. However,
its intrinsic randomness has been confirmed over and over again
by theoretical and experimental research conducted since the
first decades of the XXth century.
When designing a random number generator, it is thus a natural
choice to take advantage of this intrinsic randomness and to
resort to the use of a quantum process as source of randomness.
Formally, quantum random number generators are the only true
random number generators. Although this observation may be important
in certain cases, quantum random number generators have other
advantages. This intrinsic randomness of quantum physics allows
selecting a very simple process as source of randomness. This
implies that such a generator is easy to model and its functioning
can be monitored in order to confirm that it operating properly
and is actually producing random numbers. Contrary to the case
where classical physics is used as the source of randomness
and where determinism is hidden behind complexity, one can say
that with quantum physics randomness is revealed by simplicity.
Until recently the only quantum random number generator that
existed were based on the observation of the radioactive decay
of some element. Although they produce numbers of excellent
quality, these generators are quite bulky and the use of radioactive
materials may cause health concerns. The fact that a simple
and low cost quantum random number generators did not exist
prevented quantum physics to become the dominant source of randomness.
Optical quantum random number generator
Optics is the science of light. From a quantum physics point
of view, light consists of elementary "particles"
called photons. Photons exhibit in certain situations a random
behavior. One such situation, which is very well suited to the
generation of binary random numbers, is the transmission upon
a semi-transparent mirror. The fact that a photon incident on
such a component be reflected or transmitted is intrinsically
random and cannot be influenced by any external parameters.
The figure below schematically shows this optical system.
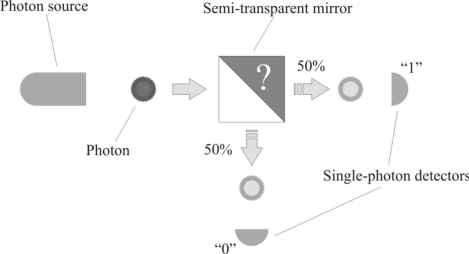
Figure 1: Optical system used
to generate random numbers.
[1] Von Neumann, J., "Various
techniques used in connection with random digits", Applied
Mathematics Serires, no. 12, 36-38 (1951).
[2] Peres, Y., Ann. Stat., 20, 590 (1992).